آموزش سودوکو| طراحی جدول| مسابقه سودوکو

این روش نوع گسترش یافته Y-Wing است. اگر بخواهیم کلیت این روش را بیان کنیم می توانیم آن را در جملات زیر خلاصه کنیم:

سه خانه که دارای سه کاندید مختلف بین خود هستند، اما خارج از مرز یک سطر، ستون یا باکس هستند. یکی از خانه ها به عنوان راس درنظر گرفته می شود که در دو عدد با دو خانه دیگر مشترک است و این خانه زانو هر سه کاندید را در خود جای داده است.

بنابراین اینگونه به نظر خواهد آمد که یکی از اعداد در این سه خانه باید مشترک باشد. همین الان شما هم فهمیدی که هدف حذف همین عدد مشترکه است.

به شکل زیر خوب دقت کن.

این روش اسمش رو به خاطر حروف X، Y و Z  گرفته. تو این روش کاندیدهای  X، Y و Z فقط در این سه خونه قرار دارند و هیچ کاندید دیگری نمیتونه تو این سه خونه باشه. نوع آرایش این روش اینه که باید یک خانه با سه کاندید داشته باشی (خانه A2 در شکل بالا)، حالا تو همون باکس خانه دیگری (خانه B3) تنها دارای دو کاندید است که هردوشون همون اعدادی هستند که کاندیدهای خانه اولی (خانه A2) بودند. حاالا در یک باکس دیگه در امتداد خانه زانویی (خانه A2) چه در سطر و یا ستون خانه دیگری است که اتفاقاً اون هم دارای دو کاندید است به هر دو کاندید اون با اعداد خانه اولی ما همخونی داره، اما همون دوتای قبلی نیستند. طبیعتاً هر جوری حساب کنید بالاخره یک عدد این وسط مشترک میشه. این عدد مشترک کلید این روش است.

مجدداً شکل بالارو نگاه کنید. حالا دیگه ساختار رو فهمیدی چیه، پس میریم سراغ استدلال این روش:

1. فرض کنید خانه زانویی (خانه A2 در شکل بالا) X باشه، بنابراین خانه B3 یا همون ضلع دوم باید Z بشه چون X قبلاً در جای دیگر انتخای شده و از کاندیدهای این خونه حذف میشه. پس قطعاً میدونیم که خانه های A1 و A3 نمیتونند Z باشند (Zهای قرمز رنگ شکل بالا)، به همون دلیلی که B3 نمیتونست دیگه X باشه.

2. حالا فرض کنید خانه زانویی (A2) این بار Y باشه، بنابراین خانه A5 که در امتداد این خانه است کاندید Y از اون حذف شده و قطعاً Z خواهد بود. بنابراین این بار هم خانه های A1 و A3 نمی تونند Z باشند (Zهای قرمز رنگ شکل بالا)

3. اگر هم که خانه A2 این بار Z باشه که دیگه اصلاً بحثی توش نیست.

خوب حالا منطق رو که فهمیدیم، استدلال رو هم که خودمونم بلد بودیم انجام بدیم، حالا باید Z مشترک رو از کدوم خونه ها حذف کنیم!؟

اینم خودتون زودتر از من فهمیدید. پس یکبار با هم مرور کنیم:

در روش XYZ-Wing سه کاندید در یک خانه پیدا می کنیم که دو کاندید اونها با یک خانه دیگه در همون باکس مشترک هستند و دو کاندید دیگه (که طبیعتاً یک عدد مشترک میمونه این وسط) هم به یک خانه دیگه در امتداد سطر یا ستون منتهی به خانه راس مشترک هستند. حذف کاندید در تنها در باکسی صورت می گیرد که خانه زانویی در آن است و تنها در خانه هایی عدد مشترک حذف می شود که در امتداد خانه ای است که در باکس مجاور در امتداد سطر یا ستون منتهی به خانه راس قرار دارد.

یعنی اگه کاندید Z بتونه در خانه های B1، B2، C1، C2 و C3 کاندید باشه با این روش نمیتونیم اونهارو حذف کنیم. چرا؟

جون در راستای خانه سوم یعنی A5 فرار ندارند.

حالا شاید شما با خودتون بگید که این همه استدلال و منطق برای همین حذف کوچیک! در جواب باید گفت که هرچه سودوکو سخت تر بشه و تکنیک ها سطح بالاتر بشن، هم خود تکنیک پیدا کردنش مشکله و هم اینکه اگه پیدا بشه کاندیداهای کمی رو حذف میکنه. البته اکثر تکنیکها کاندیدهای کمی رو حذف میکنند اما در تکنیک های حرفه ای پیدا کردنشو مشکل تر است.

قطعاً شما فرق این روش رو با Y-Wing فهمیدید، در اونجا ما یه خانه داریم اما کاندیدها دو به دو در خانه ها بودند و دو کاندیدای خانه راس در دو خانه دیگر پخش شده بود و کاندید سوم باید حزف می شد. اگه یادتون رفته یه سری به Y-Wing بزنید.

حالا چند مثال رو با هم بررسی کنیم تا خوب جا بیفته.

به شکل زیر نگاه کن.

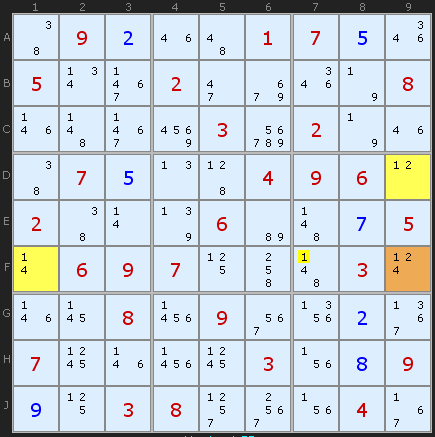
در این شکل کاندید مورد نظر عدد 1 است و خانه زانویی یا راس F9 است. این خانه با سه کاندید 1، 2 و 4 در 1/2 با خانه D9 و در 1/4 با خانه F1 مشترک است. طبق این روش و با توضیحات بالا، کاندید 1 از خانه F7 جدول ( همون عدد 1 زرد رنگ شکل بالا) حذف میشه. حالا میخوام یه مدل دیگه تحلیلش کنم که شاید شما اینطوری ندیده باشید. اگه فرض کنیم هر کدام از خانه های D9 و یا F1 به طور مجزا (یعنی یکبار D9 و یکبار F1 نه اینکه همزمان) 1 باشند در این صورت قطعاً خانه F7 نمیتونه 1 باشه. حالا یکبار فرض کنید خانه D9 عدد 2 باشه، در اینصورت کاندید 9 از خانه راس یا همون F9 حذف میشه و در این خانه تنها زوج 1/4 میمونه که حالا با زوج 1/4 خانه F1 تکنیک جفت های عریان رو تشکیل می دهند که نتیجه اون حذف عدد 1 از خانه های F5 و F7 هست. به F7 کاری نداریم چون جزء تحلیل ما نیست و حذفش غلط هم هست اما F5 دیگه کاندید 1 نداره. حالا این بار فرض کنید F1 عدد 4 باشه. بنابراین عدد 4 از کاندیدهای خانه راس یا همون F9 خارج میشه و تنها زوج 1/2 در این خونه میمونه که با زوج 1/2 خانه D9 تشکیل تکنیک جفت های عریان رو میدن که نتیجه اون حذف کاندید 1 از خانه های E7 و F7 هست. با E7 کاری نداریم جون در تحلیل ما جا نداره و اساساً حذفش هم منطقی با خود نداره اما خانه F7 این بار هم نتونست 1 باشه. یعنی ما با چهار احتمال جدا به این نتیجه رسیدیم که کاندید 1 نمیتونه در خانه F7 جدول رار بگیره، همین.

یک مثال دیگه هم با هم بررسی کنیم.

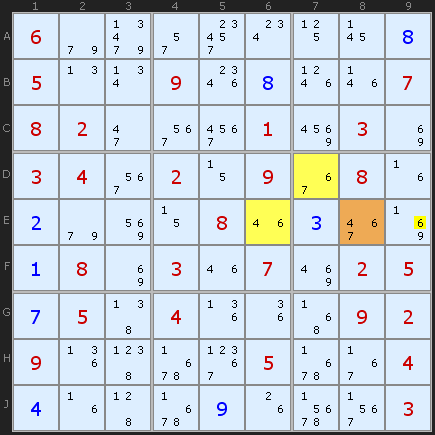
خانه راس که نارنجی هم هست همون E8 با کاندیدهای 4، 7 و 6  است که عدد 6 مشترک است. خانه راس با خانه D7 در همان باکس در کاندیدهای 7/6 و با خانه E6 در باکس مجاور در کاندیدهای 4/6 مشترک است. تحلیل اینکه چرا کاندید 6 از خانه E9 حذف میشه رو به عهده خودتون میزام. اگه سوالی داشتید مطرح کنید.

کل روش همین بود. حالا کی میگه سخته!!